Simple Harmonic OscillationsSimple Harmonic Oscillations

SHM definitions:

Displacement: distance from the equilibrium position
Amplitude: the maximum displacement from the equilibrium position
Period: the time taken to complete one full oscillation
Frequency: the number of complete oscillations per unit time

Angular frequency describes how quickly an object oscillates.

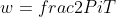
$w = frac{2Pi }{T}$

w = 2Pi f

The defining equation of simple harmonic motion is:

$a = -w^{2}x$

The acceleration is proportional to the displacement and is in the opposite direction. There are two commonly used solutions to this equation:

x=Acos (wt)

x = A sin(wt)

The velocity of an oscillator undergoing SHM is given by: $v=pm sqrt{A^{2}-x^{2}}$

From this equation it follows that velocity can vary between 0 (at ) to its maximum values, (at the equilibrium position). It follows that:

$v_{max}=wA$

The period T of a simple harmonic oscillator is independent of the amplitude A of the oscillator. Such an oscillator is described as isochronous. The shape of a graph of displacement against time is sinusoidal. If no energy is transferred to the surroundings, the amplitude remains constant. The gradient of the displacement-time graph is equal to the velocity, and the gradient of the velocity-time graph is equal to the acceleration.