Blog

Atomic Structure and Periodicity

by | Feb 7, 2024

Electromagnetic Radiation (EMR)

  • EMR: energy that exhibits wavelike behavior and travels thru space at the speed of light in a vacuum

    • Ex: light from the sun, X-rays
    • All EMR travel at speed of light
    • Each form of EMR is only different in wavelength

  • Photon: tiny particle of light that acts as a carrier of energy

  • Shorter wavelength = higher frequency = more energy
    • So there is an inverse relationship between wavelength and frequency

Essential Formulas

  • Formula: 

3 Characteristics of Waves

Wavelength Frequency Speed of light
● Distance between two consecutive peaks

● Unit = Meters
      ○ Is often given in nm but must always beconverted

          ■ 1m = 10⁹ nm

 ● The number of waves(cycles) per second

● Unit = s⁻¹ (Hertz)

 ● 2.9979 X 10⁸

Albert Einstein

  • The intensity of light is a measure of the number of photons in a beam
    • Greater intensity = more photons are available to release electrons
  •    
  • Mass (kg) of a particle:
    • v = velocity
    • Can also use equation to calculate wavelength of a particle

The Dual Nature of Light: EMR can show both wave properties and particulate matter properties

  • Electrons seem to move in an interference pattern (like a wave) and have the ability to carry energy and momentum when in motion (like a particle) → an electron is both a wave and particle

The Bohr Model

  • Predicted that electrons orbit the nucleus at fixed radii
    • Atoms absorb energy in the form of electromagnetic radiation → electrons move to higher energy lvl
  • As electrons become more tightly bound, its energy becomes more negative
    • As the electron is brought closer to the nucleus, energy is released from the system
  • Is wrong bcuz does not take into account for sublevels (s, p, d, f), orbitals, or electron spin → electrons aren’t actually locked into orbits

The Quantum Mechanical Model of the Atom

  • Quantum Mechanical Model: specifies the probability of finding an electron in the 3D space

  • Wave function of an electron: the amplitude where an electron can stay in an atom

    • Square of the wave function = the probability of the electron in the orbital

 

Shell Subshell Orbital
Pathway followed by an electron around the atom’s nucleus

Given n

Can hold max 32 e

 Pathway an electron moves inside the shell

Given l

Maximum e- depends on type of subshell

 Most probable location to find an electron and its spatial distribution

Given m

Can hold max 2 e-

Energy of a orbital is determined by its value of n → all orbitals with the same value of n have the same energy (are said to be degenerate)

Orbital configurations determine the shape of a molecule → determines their properties and how they behave

 

Heisenberg Uncertainty Principle

  • Says that it’s impossible to know the exact motion/position of an electron as it moves around the nucleus
  • Two types of electron motions in an atom
    • Orbit motion around a nucleus
    • Magnetic motion created by the spin on its axis
  • The probability of finding the electron at a specific position is greatest the closer it is to the nucleus

Different Types of Wave Functions

S Sublevel P Sublevel D Sublevel F Sublevel
1 orbital = max 2 electrons → the simplest 3 orbitals = max 6 e-

There are 3 P orbitals because are talking about 3D space → can be one orbital on the x-axis, y-axis, and z-axis

     ● Each axis canhold a total of 8electrons (s=2 &p=6)→ octet rule

 5 orbitals → max 10electrons 7 orbitals → max 14electrons

Quantum Numbers

  • Each of these orbitals is characterized by a series of numbers called quantum numbers
Name Symbol Allowed Values Notes
Principle quantum Number n 1, 2, 3, 4, … Describes the size and energy level of an orbital + relative distance from nucleus

Is equal to the number of sublevels

  • Ex: n = 2 (2nd electron shell) → 2s & 2p orbitals

n increases → orbital becomes larger = higher energy electrons
Angular momentum/azimuthal quantum number 1 0 ≤ L ≤ n-1 Describes the shape of an orbital

L = 0 → s orbital L = 1 → p orbital L = 2 → d orbital L = 3 → f orbital

L ≤ n-1

● Ex: n = 2

  • L = 0 → s sublvl
  • L = 1 → p sublvl
Magnetic quantum number m L ≤ m ≤ L Describes the orientation of the orbitalTo determine value, draw orbitals → place electron → ans will be where the last electron is

Ex:

● S sublvl has 1 orbital and l = 0→ m = 0

● P sublvl has 3 orbitals & l = 1→ -1 ≤ m ≤1
Spin quantum number m +½. -½ Describes the spin of an e-→ an e- can only spin in a clockwise or counter-clockwise direction

+ ½ ( up arrow) or -½ (down arrow)

Answer will be the spin of the last electron placed

Example: 2p⁵ → find n, l , m◻, m◻

  • N =2
  • L =1
  • m◻→ 0
  • Ms → -½

Important Principles  

  • Pauli Exclusion Principle: two electrons which share an orbital cannot have the same spin → have different values of m◻

  • Aufbau principle: electrons are placed in orbitals, shells, and subshells of increasing energy                                                     

  • Hund’s rule: Every orbital in a sublevel is singly occupied before any orbital is doubly occupied + All of the electrons in singly occupied orbitals have the same spin

    • Because of the symmetrical distribution of electrons, orbitals in which the subshell is exactly half-filled or filled are more stable → so removing an electron from these atoms requires more energy

Radial Probability, Penetration, and Electron Repulsion

  • Electrons are attracted to the nucleus at the same time as electrons repel each other.

  • Penetration: The ability of an electron to get close to the nucleus

    • Penetration depends on the shell (n) and subshell (ml)
      • Within same shell value (n), penetrating power follows trend in subshells (ml)
        • s>p>d>f
      • For different shall values and subshell (l), penetrating power follows this trend
        • 1s>2s>2p>3s>3p>4s>3d>4p>5s>4d>5p>6s>4f….
    • The closer an electron comes to the nucleus/more it penetrates → the stronger its attraction to the nucleus
    • Penetration and shielding result in an Effective force that holds the outer electrons to the atom

Electron Shielding

  • Shielding: describes the blocking of the attraction between valence electrons and nucleus by the inner-shell electrons

    • Results from balance between attractive and repulsive forces

Writing electron configuration

● Electron configuration: tell us where electrons are approx

               ○ For D block elements, count starting from S block

● Noble gas Configuration: consists of the elemental symbol of the last noble gas prior to that atom, followed by the configuration of the remaining electrons

               ○ Use as shortcut → on AP exam can always use

● Ex:

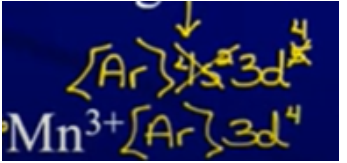
Ion Configurations

  • Electrons are removed/added to the valence energy lvl first → only then can e- be removed/added from the d sublvl
  • Ex: 

Write out configuration for pure element first and then remove/add electrons

  • Can’t just keep noble gas in brackets → have to back up to noble gas before